人脸识别
在人脸识别的任务中,特征不仅仅是要可分,而且还要能够容易判别,如下图,左边的特征虽然可分,但是类间距离不够大,因此会导致错分现象,而好的特征应该像右图那样,很容易区分。 即减小类内距离,增加类间距离。
在人脸认证任务中,常用的步骤是通过提取网络最后一层特征,通过计算余弦或者欧式距离进行判断。

Center Loss
论文链接:A Discriminative Feature Learning Approach for Deep Face Recognition
代码链接:https://github.com/ydwen/caffe-face
主要贡献
Softmax函数学习到的特征仍然有很大的类内差距,提出了一种新的辅助损失函数(center loss),结合 softmax交叉熵损失函数,在不同数据及上提高识别准确率。
Sotfmax损失函数公式:
\[L_S=-\sum_{i=1}^{m}\log{\frac{e^{W_{y_i}^T x_i+b_{y_i}}}{\sum_{j=1}^{n} e^{W_j^T x_i+b_j}}}\]Softmax使得每一类可分,关注的是类间的距离,但并没有关注类内的问题。因此作者希望在每一个batch中,每一个样本都能向同一类的中心靠拢。即在分类时,也要向类心靠近,Loss如下:
\[L_C=\frac{1}{2}\sum_{i=1}^{m}\left \| x_i-c_{y_i} \right \|_2^2\]$C_{y_i}$表示属于$y_i$类的特征的中心。
这样做是存在问题的:
理想情况下,我们每次更新权值都要遍历全部的训练集去获得每个类的中心,这是低效甚至不实际的
为了解决这个问题,作者使用了minbatch中的每个类的中心来更新,(虽然这样可能有些类的中心在一次迭代中无法更新到)
\[\Delta c_j=\frac{\sum_{i=1}^{m}\delta(y_i=j)\cdot(c_j-x_i) }{1+\sum_{i=1}^{m}\delta(y_i=j)}\]总损失函数使用的是Softmax+center Loss联合损失:
\[L=L_S+\lambda L_C =-\sum_{i=1}^{m}\log{\frac{e^{W_{y_i}^T x_i+b_{y_i}}}{\sum_{j=1}^{n} e^{W_j^T x_i+b_j}}}+ \frac{\lambda}{2}\sum_{i=1}^{m}\left \| x_i-c_{y_i} \right \|_2^2\]求导:
\[\frac{\partial{L_C}}{\partial {x_i}}=x_i-c_{y_i}\]算法流程类似一般的卷积神经网络,就是多了一个更新中心点的流程。
NormFace
论文链接:NormFace: L2 Hypersphere Embedding for Face Verification
主要贡献
解决了4个问题:
1.为什么在测试时必须要归一化?
2.为什么直接优化余弦相似度会导致网络不收敛?
3.怎么样使用softmax loss优化余弦相似度
4.既然softmax loss在优化余弦相似度时不能收敛,那么其他的损失函数可以收敛吗?
问题分析
之前的人脸识别工作,在特征比较阶段,通常使用的都是特征的余弦距离,而余弦距离等价于L2归一化后的内积,也等价L2归一化后的欧式距离(欧式距离表示超球面上的弦长,两个向量之间的夹角越大,弦长也越大)。然而,在实际上训练的时候用的都是没有L2归一化的内积
关于这一点可以这样解释,Softmax函数是:
\[P_{y_i}={\frac{e^{W_{y_i}^T x_i+b_{y_i}}}{\sum_{j=1}^{n} e^{W_j^T x_i+b_j}}}\]可以理解为$W_{y_i}$和特征向量$x_i$的内积越大,$x_i$属于第$y_i$类概率也就越大,训练过程就是最大化x与其标签对应项的权值$W_{label(x)}$的过程。
这也就是说在训练时使用的距离度量与在测试时使用的度量是不一样的。
作者实验说明进行人脸验证时使用归一化后的内积或者欧式距离效果明显会优于直接计算两个特征向量的内积或者欧式距离。

注意这个Normalization不同于batch normalization,一个是对L2范数进行归一化,一个是均值归零,方差归一。
是否可以直接在训练时也对特征向量归一化?
针对上面的问题,作者设计实验,通过归一化Softmax所有的特征和权重来创建一个cosine layer,实验结果是网络不收敛了。
问题1、2为什么必须要归一化和为什么直接优化归一化后的特征网络不会收敛
全连接层特征降至二维的MNIST特征图:
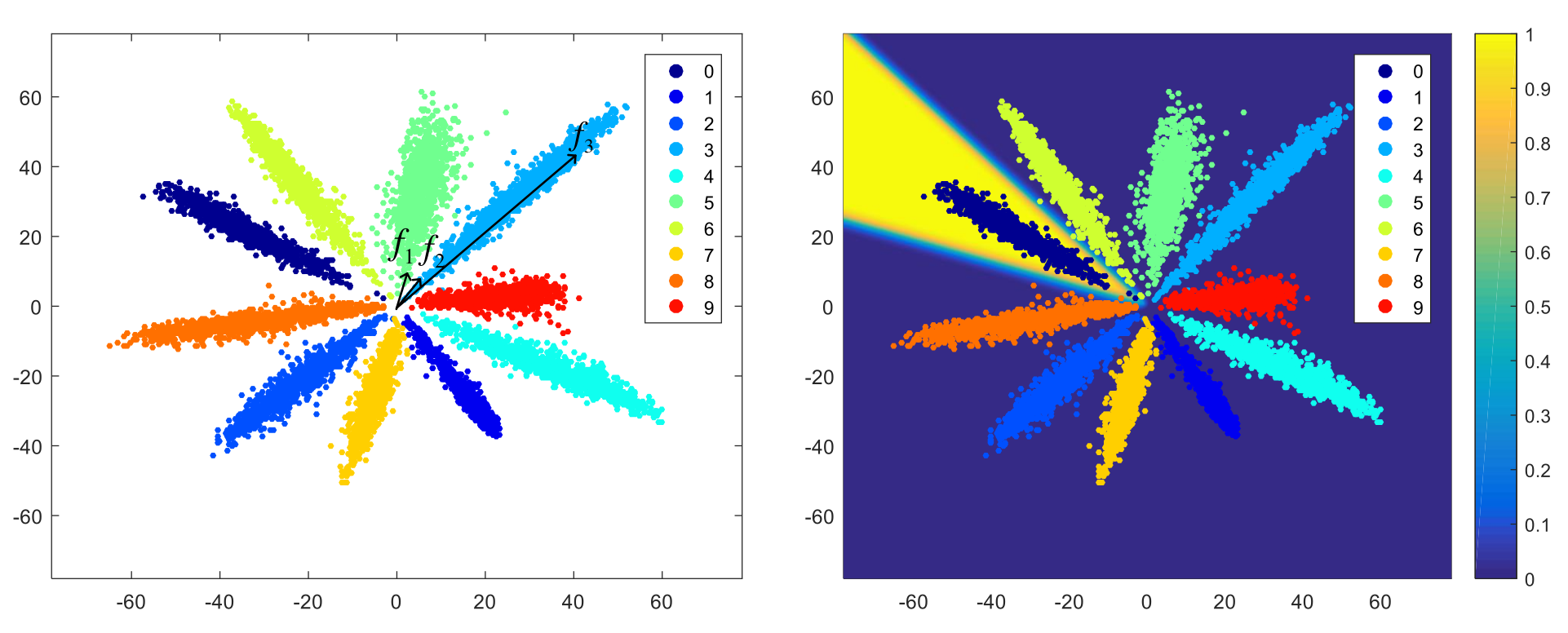
左图中,f2 f3是同一类的两个特征,但是可以看到f1和f2的距离明显小于f2 f3的距离,因此假如不对特征进行归一化再比较距离的话,可能就会误判f1 f2为同一类。
为什么会是特征会呈辐射状分布
\[P_{y_i}={\frac{e^{W_{y_i}^T x_i}}{\sum_{j=1}^{n} e^{W_j^T x_i}}}\]Softmax实际上是一种(Soft)软的max(最大化)操作,考虑Softmax的概率,假设是一个十个分类问题,那么每个类都会对应一个权值向量$W_0,W_1…W_9$,某个特征f会被分为哪一类,取决f和哪一个权值向量的内积最大。对于一个训练好的网络,权值向量是固定的,因此f和W的内积只取决与f与W的夹角。也就是说,靠近$W_0$的向量会被归为第一类,靠近$W_1$的向量会归为第二类,以此类推。网络在训练过程中,为了使得各个分类更明显,会让各个权值向量W逐渐分散开,相互之间有一定的角度,而靠近某一权值向量的特征就会被归为相应的类别,因此特征最终会呈辐射状分布。
如果添加了偏置结果会是怎么样的?
\(P_{y_i}={\frac{e^{W_{y_i}^T x_i+b_{y_i}}}{\sum_{j=1}^{n} e^{W_j^T x_i+b_j}}}\)
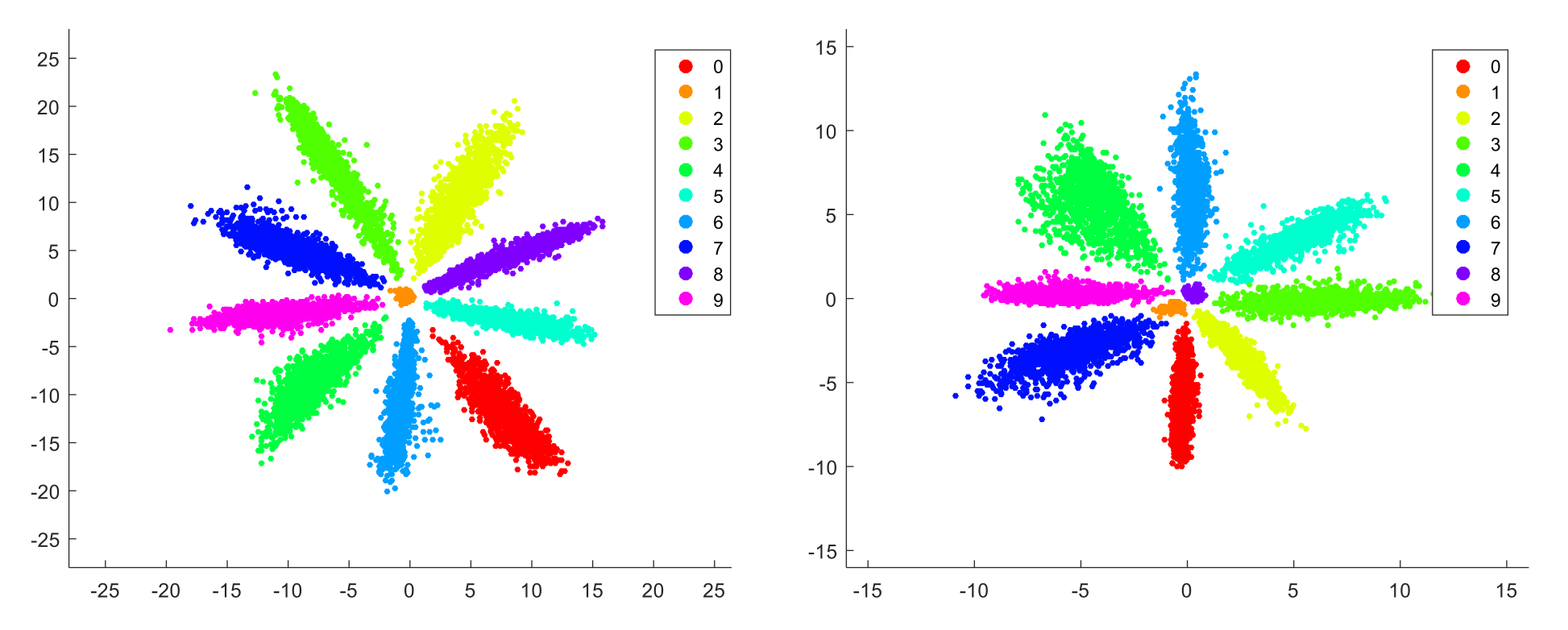
如果添加了偏置,不同类的b不同,则会造成有的类w角度近似相等,而依据b来区分的情况。在这种情况下如果再对w进行归一化,那么中间这些类会散步在单位圆上各个方向,造成错误分类。
所以添加偏置对我们通过余弦距离来分类没有帮助,弱化了网络的学习能力,所以我们不添加偏置。
网络为何不收敛
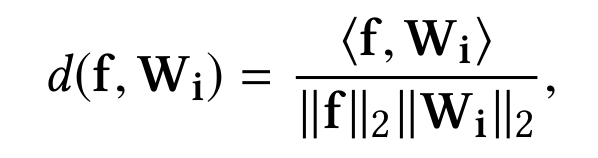
是一个[-1,1]区间的数,经过softmax函数之后,即使各个类别都被完全分开了(即f和其标签对应类的权值向量$W_f$的内积为1,而与其他类的权值向量内积都是-1),其输出的概率也会是一个很小的数:
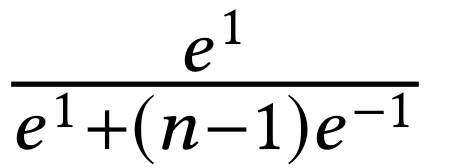
上式在n=10时,结果为0.45;在n=1000时,结果为 0.007,非常之小。因此即使对于完全分开的类,由于梯度中有一项是(1-y),其梯度还是很大,因此无法收敛。
为了解决这一问题,作者提出了一个关于Softmax的命题来告诉大家答案。
命题:如果把所有的W和特征的L2norm都归一化后乘以一个缩放参数L,且假设每个类的样本数量一样,则Softmax损失下界(在所有类都完全分开的情况下)是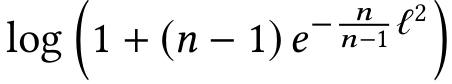
因此,在归一化层后添加一层放大层l可以解决无法收敛的问题。
归一化层的定义
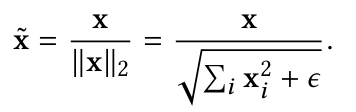
改进度量学习
借助于以上对Softmax的透彻研究,作者顺手改进了一下度量学习通常要使用两个损失函数contrastive loss与triplet loss
公式证明见论文
Large-Margin Softmax Loss
论文链接:Large-Margin Softmax Loss for Convolutional Neural Networks
MxNet代码链接:https://github.com/luoyetx/mx-lsoftmax
主要贡献
提出一种基于Margin的L-Softmax损失函数,可以明确地促使学习到的特征具有类内的紧凑性和类间的可分离性。此外L-Softmax不仅可以调节所需的Margin,还可以避免过拟合的发生。
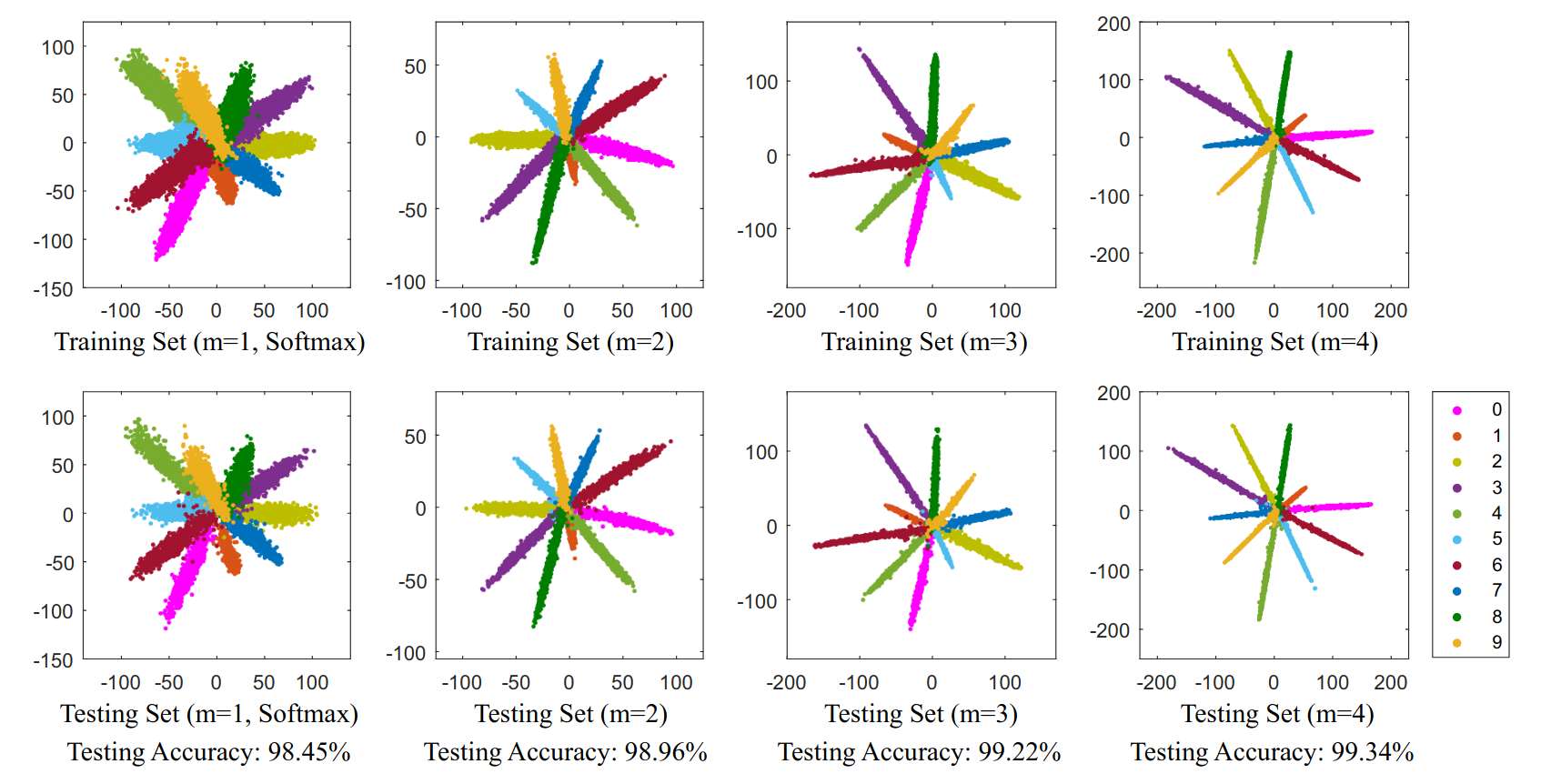
L-Softmax出发点也是类内压缩和类间分离,对于softmax loss,向量相乘可以转化为cos距离。
softmax loss可改写为:
\[L_S=-\log{\frac{e^{W_{y_i}^T x_i}}{\sum_{j=i}^{n} e^{W_j^T x_i}}}\\ =-\log{\frac{e^{\left \| W_{y_i} \right \|\left \| x_i \right \|cos(\theta_{y_i})}}{\sum_{j} e^{\left \| W_j \right \|\left \| x_i \right \|cos(\theta_j)}}}\]假设一个2分类x属于1,那么softmax希望$W_{1}^{T}x>W_{2}^{T}x$,等效
$\left | W_1 \right |\left | x \right |cos(\theta_1)>\left | W_2 \right |\left | x \right |cos(\theta_2)$
为了使上面的不等式左边远远大于右边(促使分类更加严格),L-Softmax就是将上面不等式加约束:
$\left | W_1 \right |\left | x \right |cos(m\theta_1)>\left | W_2 \right |\left | x \right |cos(m\theta_2),(0\le\theta\le\frac{\pi}{m})$
这样产生一个决策Margin,m是正整数,可以控制Margin的大小,m越大,Margin越大,学习特征的难度越大,分类边界越严格。因此L-softmax loss的思想简单讲就是加大了原来softmax loss的学习难度。
遵照上面的规则,L-Softmax损失函数可以定义为:
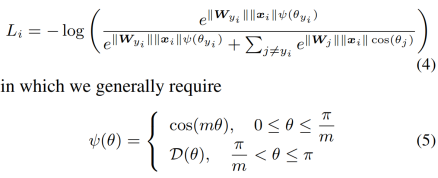
针对$\Phi$函数可简化为:
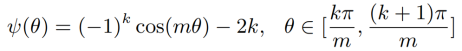
SphereFace
论文链接:SphereFace: Deep Hypersphere Embedding for Face Recognition
代码地址:https://github.com/wy1iu/sphereface
主要贡献
提出了angular softmax loss(A-softmax loss)简单讲就是在large margin softmax loss的基础上添加了两个限制条件$\left | W \right | =1$和$b=0$,使得预测仅取决于W和x之间的角度。
softmax公式:
\[L=\frac{1}{N}\sum_iL_i=\frac{1}{N}\sum_i-\log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}})\]其中$L_i$
\[L_i=-\log{\frac{e^{W_{y_i}^T x_i+b_{y_i}}}{\sum_{j=i}^{n} e^{W_j^T x_i+b_j}}}\\ =-\log{\frac{e^{\left \| W_{y_i} \right \|\left \| x_i \right \|cos(\theta_{y_i})+b_{y_i}}}{\sum_{j} e^{\left \| W_j \right \|\left \| x_i \right \|cos(\theta_j)+b_{j}}}}\]引入限制条件$\left | W_1 \right |=\left | W_2 \right |=1$和$b_1=b_2=0$
\[L_{modified}= \frac{1}{N}\sum_i-\log{\frac{e^{ \left \| x_i \right \|cos(\theta_{y_i},i)}}{\sum_{j} e^{\left \| x_i \right \|cos(\theta_j,i)}}}\]为什么引入限制?
以2分类为例,原来的分类边界为$({W_1-W_2})x+b_1-b_2=0$,添加限制后变成$\left | x\right|(cos\theta_1-cos\theta_2)=0$
也就是说边界的确定变成只取决于角度了,这样就能简化很多问题。
在这两个限制条件的基础上,作者又添加了和large margin softmax loss一样的角度参数
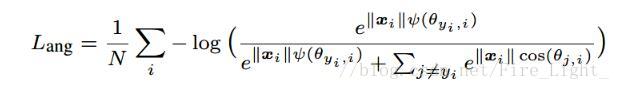
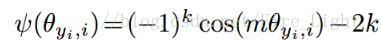
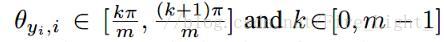
A-Softmax的性质
性质一: A-Softmax Loss定义了一个大角度间隔的学习方法,m越大这个间隔的角度也就越大,相应区域流形的大小就越小,这就导致了训练的任务也越困难。
性质二:
二分类问题中:$m_{min}\gt2+\sqrt{3}$,多分类问题中:$m_{min}\ge3$
CosFace|AMSoftmax
论文链接:CosFace: Large Margin Cosine Loss for Deep Face Recognition
论文链接:Additive Margin Softmax for Face Verification
两篇工作基本一致
主要贡献
Large Margin Cosine Loss (LMCL):Cosine空间上的损失函数,将A-Softmax中的θ乘以m,改为了对cos(θ)减去余弦间隔m(additive cosine margin),还对特征向量和权重归一化。
一句话介绍完这篇paper的创新点就是将angular softmax loss中的loss设计进行了以下替换:
A-softmax loss:$cos(m\theta_1)=cos(\theta_2)$
Large Margin Cosine Loss:$cos(\theta_1)-m=cos(\theta_2)$
然后根据Normface,对f进行归一化,乘上缩放系数s,最终的损失函数变为:
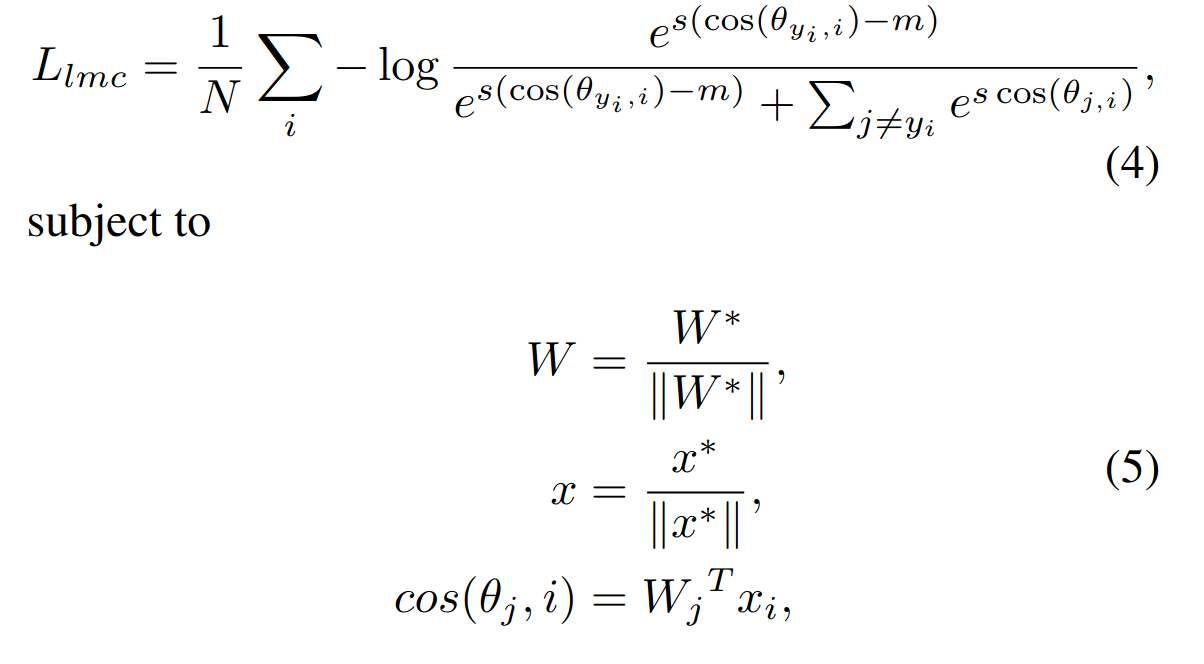
原因是作者认为由于余弦函数的非单调性,A-softmax loss较难优化,A-softmax loss为了解决这问题使用了特殊的分段函数。同时A-softmax loss的决策面会依赖于$\theta$值,这使得不同的类别对应着不同的angular margin,在决策空间中,一些类间特征有着较大的margin同时另一些类间特征可能有着较小的margin,这导致特征的判别能力减弱。
ArcFace(Insight Face)
论文链接:ArcFace: Additive Angular Margin Loss for Deep Face Recognition
开源代码:https://github.com/deepinsight/insightface
主要贡献
是AmSoftmax/CosFace的一种改进版本,将m作为角度加上去了,这样就强行拉大了同类之间的角度,使得神经网络更努力地将同类收得更紧。
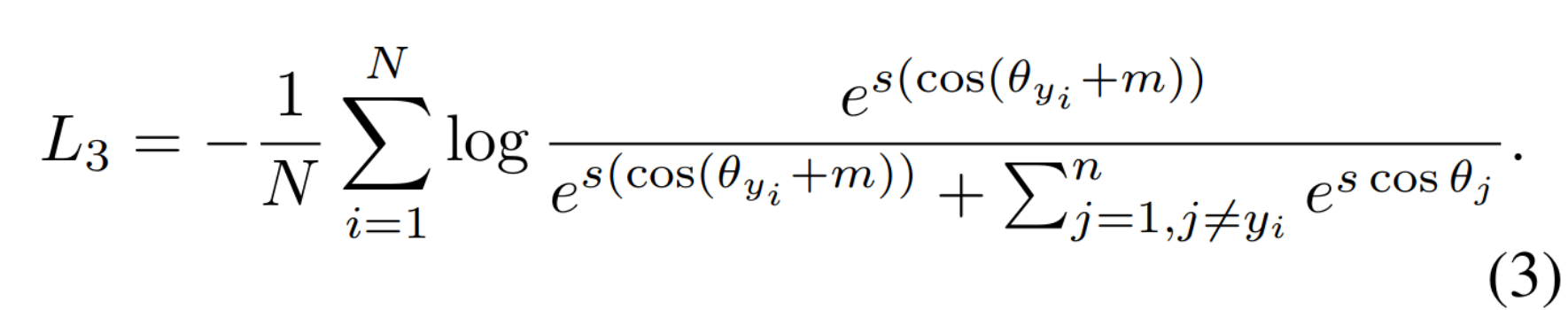
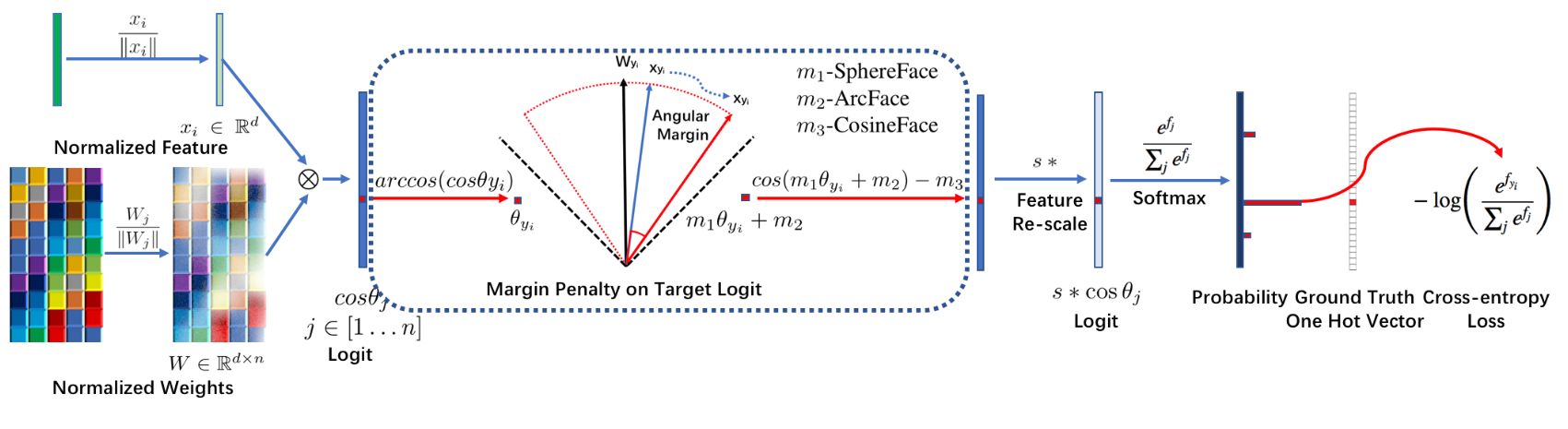
在Mxnet中伪代码实现:
1、对特征向量$x$进行$L2$归一化
2、对权重$W$ 进行$L2$归一化
3、计算$Wx$得到预测向量$y$
4、从$y$中挑出与ground truth对应的值
5、计算其反余弦得到角度
6、角度加上$m$
7、得到挑出从$y$中挑出与ground truth对应的值所在位置的独热码
8、将$cos(\theta+m)$通过独热码放回原来位置
9、对所有值乘上固定值$s$
在SphereFace、ArcFace和CosFace中,提出了三种不同的margin惩罚,分别是乘法角度间隔m1、加法角度间隔m2、加法余弦间隔m3。从数值分析的角度来看,不同的margen惩罚,无论是加上角度空间还是加在余弦空间,都通过惩罚目标逻辑(target logit),来加强类内紧度和类间多样性。