• CNN：我不是你想的那样
  • 论文思想
    • 图片高低频分离(非重点)
    • 初步实验分析
    • 提出假设
    • 实验论证假设
    • 对抗攻击和防御
  • 总结
• 噪声label学习
  • 论文思想
  • 算法流程
• 网络泛化能力
  • 论文思想
    • Randomization tests
    • The role of explicit regularization
    • Finite sample expressivity
  • 总结

CNN：我不是你想的那样

论文名称：High-frequency Component Helps Explain the Generalization of Convolutional Neural Networks

github：https://github.com/HaohanWang/HFC

每当我们训练完一个CNN模型进行推理时候，一旦出现人类无法解释的现象就立刻指责CNN垃圾，说这都学不会？其实你可能冤枉它了，而本文试图为它进行辩护。

本文是cvpr2020 oral论文，核心是从数据高低频分布上探讨CNN泛化能力，其注意到CNN具备捕获人类无法感知的高频成分能力，而这个现象可以用于解释多种人类无法理解的假设，例如泛化能力、对抗样本鲁棒性等。

本文其实没有提出一个具体的解决办法，主要是通过CNN能够捕获人类无法感知的高频成分这一现象而对所提假设进行分析。我个人觉得本文应该作为cv领域从业者的必读论文。

论文思想

图片高低频分离(非重点)

为了方便后面分析，先对图片的高低频分离过程进行说明(如果看不懂也无所谓，不影响阅读，知道啥是高低频成分就可以了)。

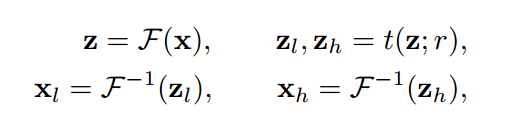表示样本对，x是图片，y是对应的标注，表示傅里叶变换，表示反傅里叶变换，表示对样本x进行傅里叶变换，z是x的频率分量，表示反傅里叶变换。而表示阈值函数，该函数通过一个半径阈值，将频率分量分成低频分量和高频分量，该阈值函数具体如下：

其中表示当前位置和中心位置之间的距离，文中用的是欧氏距离。注意在FFT频谱图中靠近中心区域是低频分量，远离中心区域是高频分量。低频成分一般就是图片纹理或者信息，高频成分就是一些边缘和像素锐变区域。

简单来说就是对一张32x32的图片进行FFT变换，输出也是32x32频谱图，其中越靠近中心越是低频成分，然后在FFP频谱图中心设置一个半径为r的圆，圆内频谱成分保留，其余成分置为0，通过逆傅里叶变换得到重建图片，该图片即为保留低频成分后的像素图。r越大，圆内保留的成分越多，信息丢失越少，重建后原图信息越多。当r比较小的时候大部分高频成分会被抛弃，重建图会非常模糊。

初步实验分析

为了引入本文论点，作者做了一个简单实验。首先用CIFAR10在训练数据训练一个resnet18分类模型，接着在测试集上进行测试，此时可以得到模型正确率，接着进一步通过傅里叶变换，把原图转换到频域，再用一个半径阈值r=12，分离出高频部分和低频部分，再对高频和低频部分进行反傅里叶变换，得到高频重建图片和低频重建图片，然后测试这两张图片。结果出现了一些非常奇怪的现象：模型对人眼看上去和原图差不多的低频图错误预测，反而正确预测了全黑的高频图。一个典型图片如下所示：

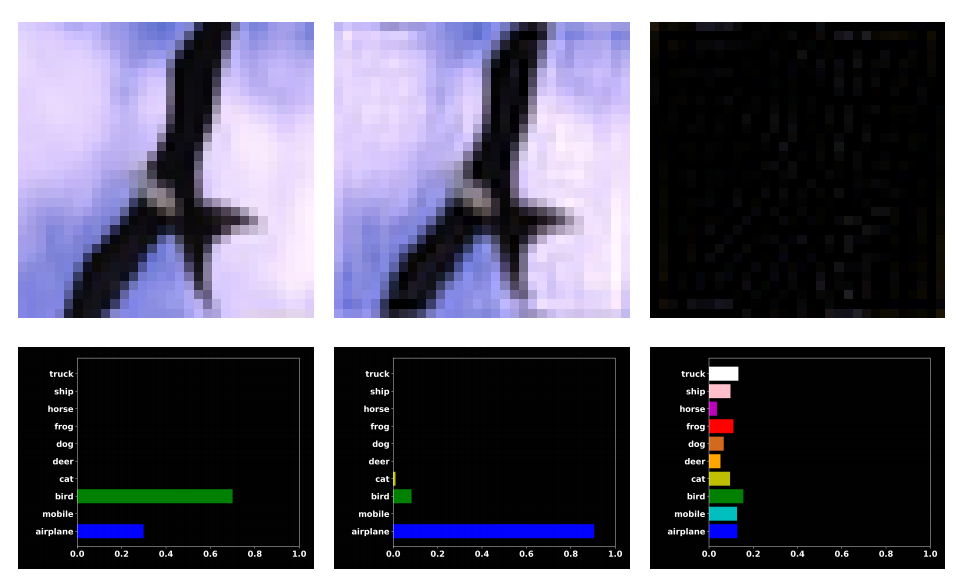
左边图是原始测试图，可以看出其很大概率认为是鸟，但是对低频成分重建图(中间图)却几乎可以肯定是飞机，高频成分重建图(右边图)到是预测为鸟，这种现象在10k张测试集中大概有600张。

这种现象完全不符合人类的认知。

提出假设

针对上述不符合常理的现象，作者提出了合理假设：人类只能感知低频分量，而CNN对低频和高频分量都可以感知，图示如下：

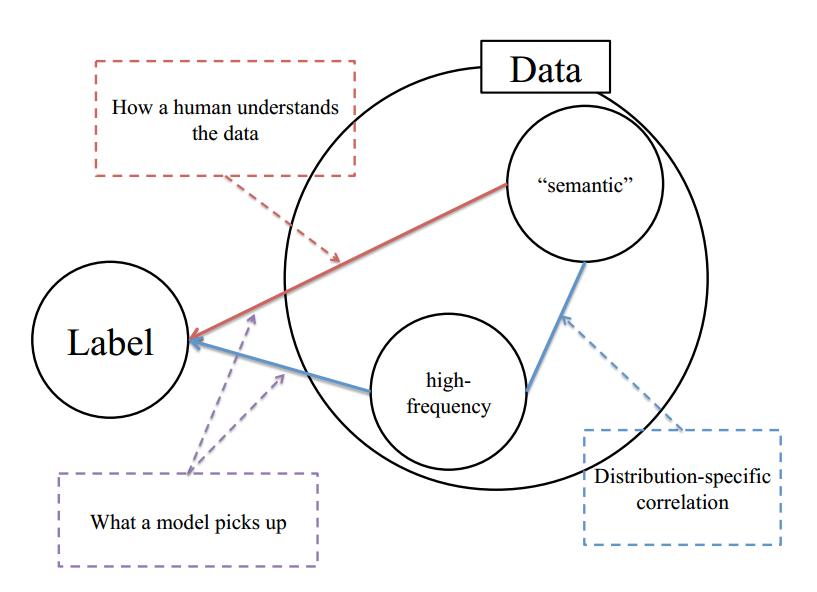
对于任何一个数据集，都应该包括语义信息(纹理信息或者说低频信息)和高频信息，只不过包括比例不定而已，并且对于同一个分布数据集，其语义分布和高频分布都应该有自己的分布特性。可以简单认为对于同一个类别标注的数据集，假设该数据集收集自多个场景，每个场景内的语义分布应该是近乎一致的(不然也不会标注为同一类)，但是高频分布就不一定了，可能和特定域有关，该高频成分可能包括和类别相关的特定信息，也可以包括分布外的噪声，并且该噪声对模型训练是有害的，会影响泛化能力。

对于人类而言，标注时候由于无法感知高频成分故仅仅依靠语义进行标注，忽略了高频成分。但是CNN训练时候会同时面对语义低频成分和高频成分，这个gap就会导致CNN学习出来的模型和人类理解的模型不一样，从而出现常规的泛化认知错误。这一切实际上不能怪CNN，而是数据分布特性决定的。

当CNN采用优化器来降低损失函数时，人类并没有明确告知模型去学习语义还是高频信号，这导致模型学习过程中可能会利用各种信息来降低损失。这样尽管模型可能会达到较高的准确率，但它理解数据的过程和人类不一样，从而导致大家认为CNN很垃圾。

而且论文中未避免被后续论文打脸，还特意指出：本文并没有说模型有捕捉高频信号的倾向性，这里的主要观点是模型并没有任何理由忽略高频信息，从而导致模型学到了高频和语义的混合信息。

实验论证假设

上述假设是作者自己提出的，为了使得假设更加可信，作者进行了后续详细实验。

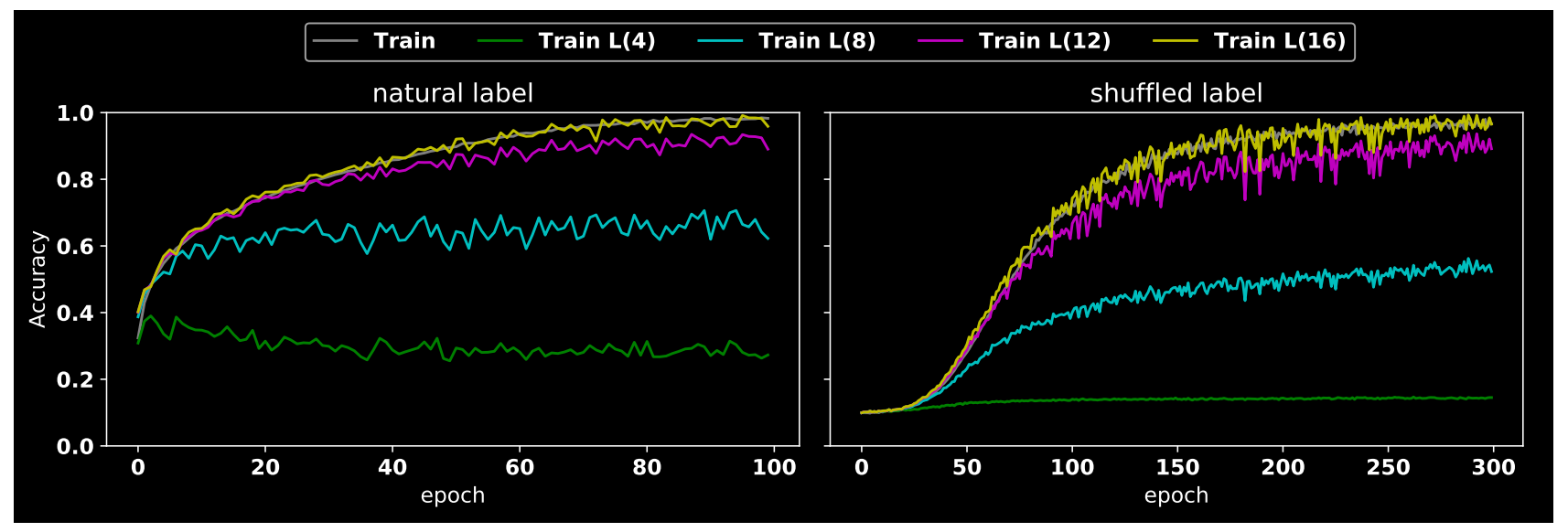
(1) nutural label VS shuffled label nutural label就是原始标注label即原始图片和label对，而shuffled label是对label随机打乱导致有些label错误的情形。将这两种数据分别在cifar10训练集上采用resnet18进行训练，训练过程acc曲线如上所示，其中L(n)表示对图片采用半径为n的阈值过滤掉高频成分，然后对保留频谱成分进行重建，注意n越大，保留的信息更多。

从图中可以看出很多重要信息，其现象具体如下：

• 从shuffled label的黄线可以看出，即使把label随机打乱，也可以得到非常高的准确率，只不过需要更多的epoch，而且震荡也比较厉害。这个现象其实在Understanding deep learning requires rethinking generalization论文中有做过相关工作
• 当半径n由小变大时候，不管是shuffled label还是natural label，acc都是从低变高
• 刚开始训练时候natural label的acc起点比shuffled label高40%

下面对上述现象进行分析：

• CNN的记忆能力很强，即使label随机打乱，acc也可以接近1。我们通常认为cnn强拟合能力把label直接记住了，但是这就出现一个问题了：既然natural label能够轻易的就记住所有label，那为何还CNN训练过程中还会考虑测试集的泛化能力呢？因为在Understanding deep learning requires rethinking generalization中提到虽然cnn可以强行记住label，但是有些模型还是有较好泛化能力的，这就解释不通了
• 上述现象如果从数据高低频角度考虑就可以解释通。因为刚开始训练时候natural label的acc起点比shuffled label高40%，所以我们可以推导：cnn在训练早期会先利用语义信息或者说低频信息进行训练，当loss不能再下降时候会额外引入高频成分进一步降低loss。因为shuffled数据集的label被随机打乱了，所以cnn无法利用语义低频信息进行训练，但是在后期开始引入高频成分从而acc最终变成1,而natural label由于有低频语义信息，故刚开始很快acc就变成40%，后面也开始引入高频信息进一步提高acc。
• 当半径n由小变大时候，不管是shuffled label还是natural label，acc都是从低变高现象出现的原因也是上述道理，因为随着r变大，高频成分保留的越来越多，cnn后期能利用的高频成分越来越多，所以loss可以不断下降

总结下：cnn训练过程会先采用低频语义信息进行降低loss，当继续训练无法降低loss时候会额外考虑高频成分进一步降低loss，而由于label被shuffle掉导致无法利用低频语义信息，则出现刚开始acc为0的现象，但是因为后期利用了高频成分，故最终还是能够完全拟合数据。

需要特别强调的是：高频成分可以分成两部分：和数据分布相关的有用高频成分A、和数据无关的噪声有害高频成分B。在natural label数据训练过程中，cnn可能会利用AB两种高频成分进行过拟合，而且由于利用的AB比例无法确定，故而就会出现CNN模型存在不同的泛化能力，如果噪声成分引入的多，那么对应的泛化能力就下降。

通过上述现象，我们很容易解释早停止手段为何可以防止过拟合，因为越到训练后期其可利用的和数据相关的有用高频成分就越少，为了降低loss，就只能进一步挖掘样本级别的特有的噪声高斯信息。

遗憾的是暂时没有一种手段把噪声高频成分过滤掉，仅仅保留有用高频成分。

(2) 低频成分 VS 高频成分

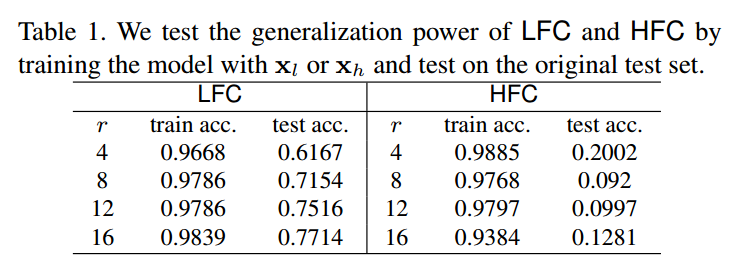
对图片进行高低频分离然后重建，得到图片，在这两种数据上训练，然后在原始数据集上测试，结果如上所示。可以得到如下结论：

• 随着r变大，由于保留的高频成分越多，所以训练集和测试集准确率都增加了，这其实说明高频成分不全是噪声，很多应该还是和数据分布相关的有用信息
• 采用低频成分训练的泛化能力远远高于高频成分训练的模型。这个现象造成的原因是label是人类标注的，人类本身就是按照低频语义信息进行标注，可以大胆猜测，如果人类能够仅仅利用高频成分进行标注，那么上述现象应该就是相反的

(3) 启发式组件通俗解释 这里说的启发式组件是指的Dropout、Mix-up、BatchNorm和Adversarial Training等，这些组件已经被证明可以提高模型泛化能力，作者试图采用本文观点进行分析成功的原因。

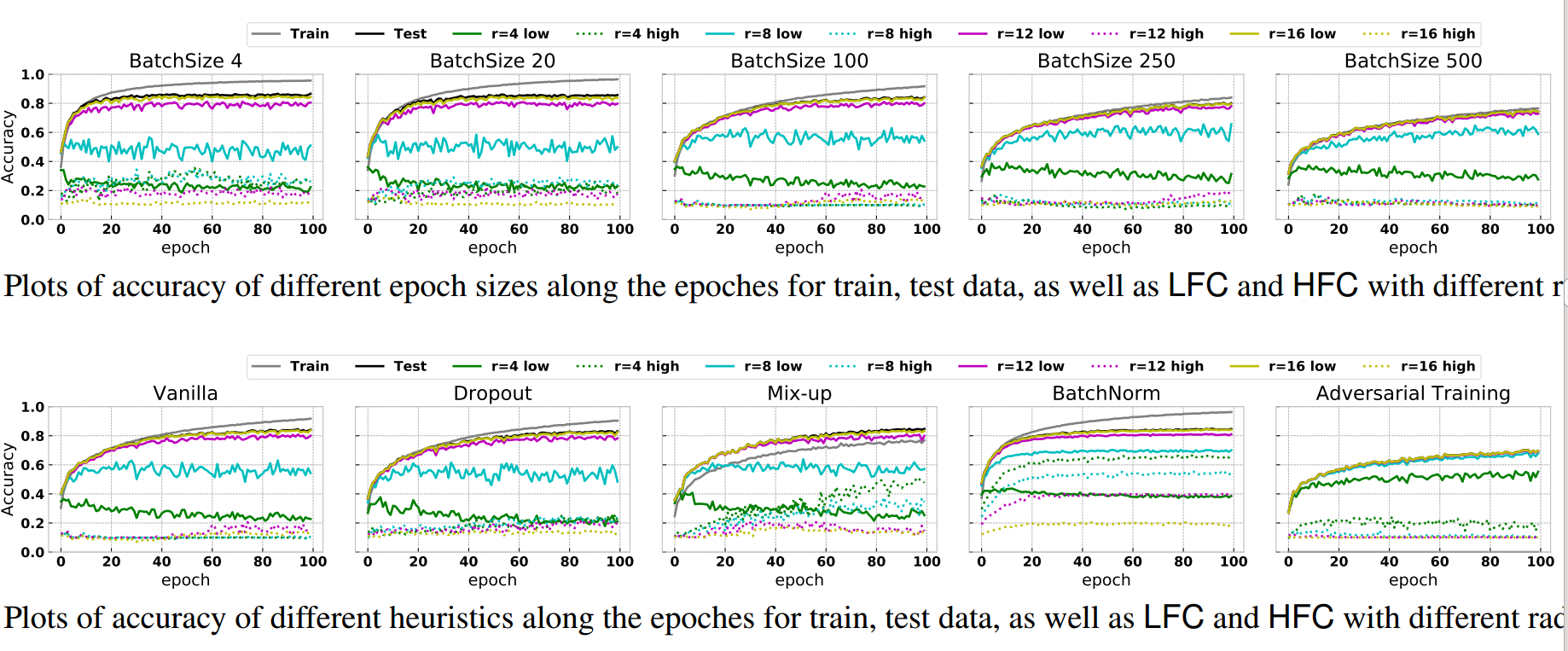
上图比较多，主要看第二行，但是可以归纳为：

• 大batch size训练时候,会同时考虑更多的非噪声的同分布高频成分，从而可以缩小训练和测试acc的误差间隔
• dropout由于加入后和不加入时候差不多，所以看不出啥规律
• 加入mixup后，训练acc和测试acc曲线gap变小，原因是mixup操作其实相当于混淆了低频语义信息，从而鼓励CNN尽可能多的去捕获高频信息
• 当引入对抗样本后，cnn精度快速下降，原因是对抗样本可能是改变了高频分布(因为人眼无法感知),而训练过程中实际上学到的高频分布和对抗样本的高频分布不一致，从而CNN会完全预测错误
• BN的分析作者单独进行分析

从以上分析可以看出，如果试图从数据的高低频分布以及CNN先学低频再学高频这个特性进行分析目前所提组件，是完全可以解释通的。

(4) BN训练过程分析

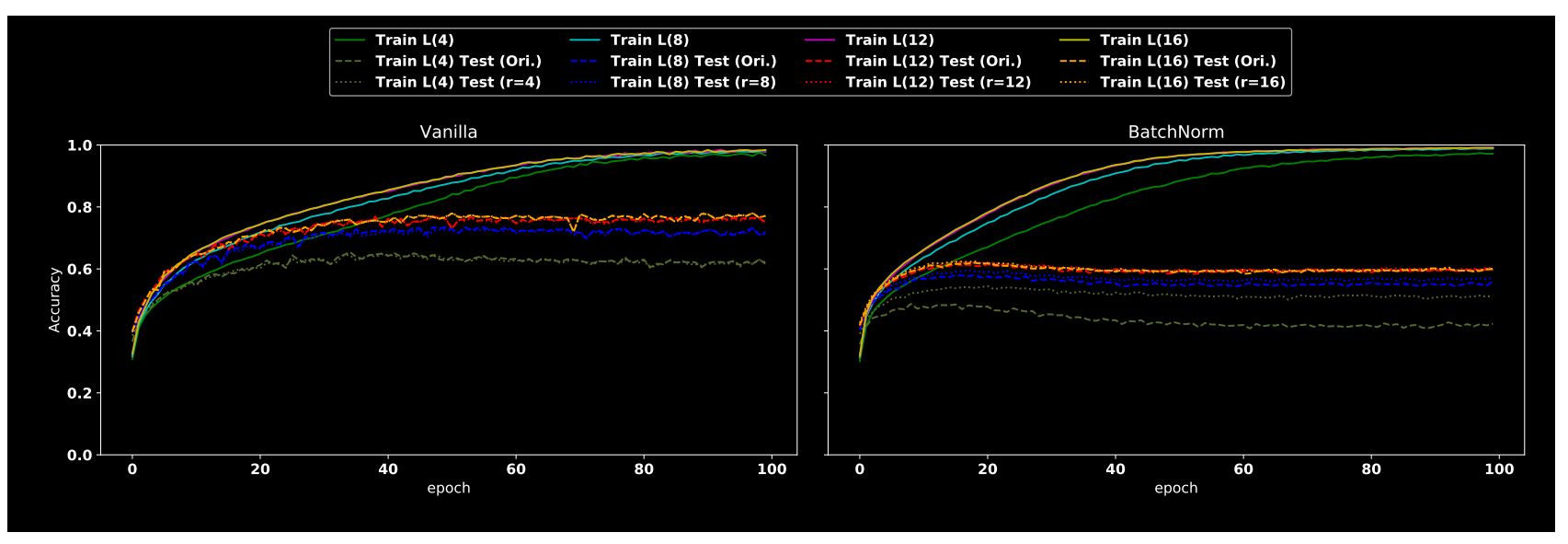
vaillla是指没有引入BN的模型。作者假设BN优势之一是通过归一化来对齐不同预测信号的分布差异，没有经过BN训练的模型可能无法轻松获取这些高频成分，而且高频成分通常是较小的幅度，通过归一化后可以增加其幅值。总之BN层引入可以让模型轻易捕获高频成分，并且由于对齐效应，大部分捕获的会是有用高频成分，从而加快收敛速度，提高泛化能力。

对抗攻击和防御

前面分析了特别多，但是除了加深对CNN的理解外，好像没有其他作用。为了消除大家对本文贡献的错觉，作者说可以将上述思想应用到对抗攻击和防御领域，加强模型鲁棒性。

前面说过对抗样本可以和高频成分联系起来，其可以认为是扰动了人类无法感知的高频成分，从而使得网络无法识别。作者首先分析对抗样本对网络造成的影响，然后提出了针对性改进。

首先采用标准的FGSM或者PGD等方法生成对抗样本，然后将对抗样本联合原始数据进行训练，最后可视化第一次卷积核参数，如下所示：

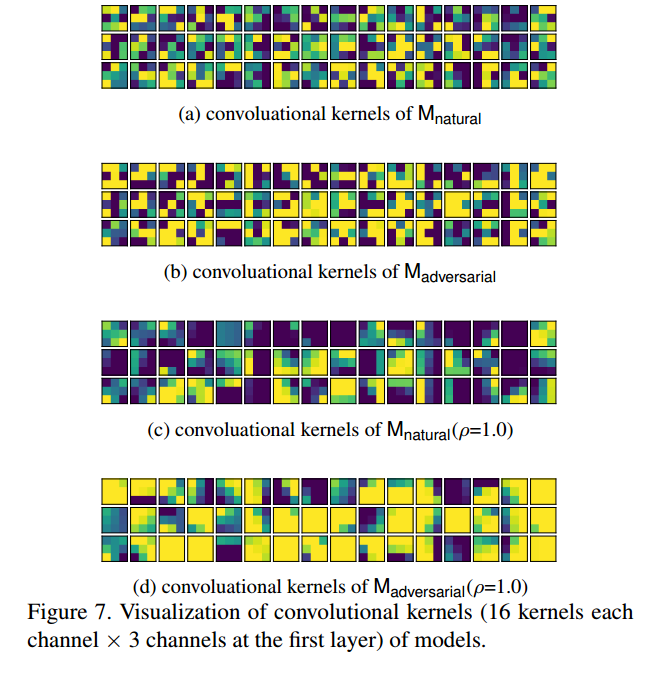
可以发现经过对抗样本训练后的模型，卷积核参数更加平衡(相邻位置的权重非常相似)。通过以前的论文也可以证明平滑卷积核能够有效地移除高频信号，从本文假设来理解上述现象就是一个非常自然的想法了。

有了上述的论证，那么我们可以试图思考：如果我直接把卷积核平滑化是不是可以提高鲁棒性？为此作者采用了如下公式：

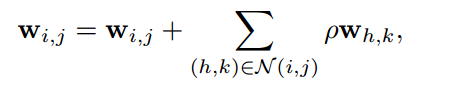
其实就是在每个位置的核参数都按照一定比例加上邻近位置的核参数，使得核参数平滑。效果如下所示：

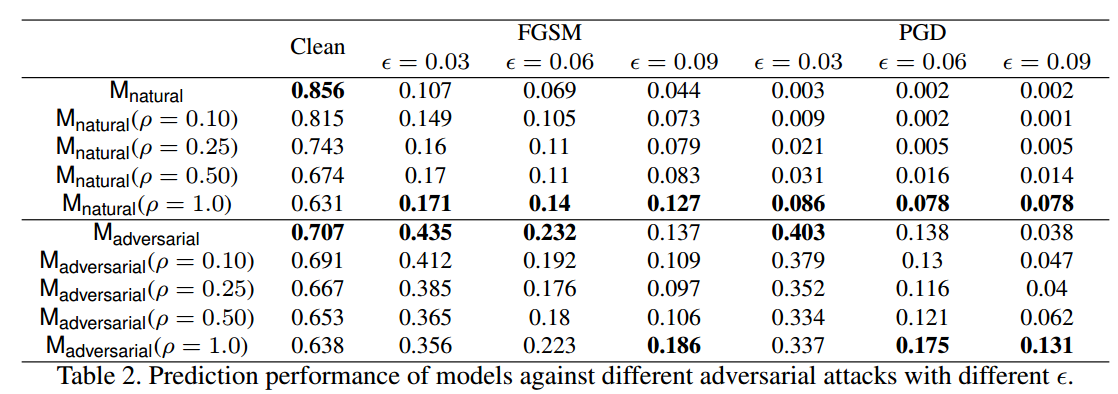
可以发现当应用平滑方法时，CNN精度的性能下降非常多，但是对抗鲁棒性提高了一点。这个小实验可以说明几点：

• 当核参数平滑后，会过滤掉图片的高频成分，导致acc急剧下降
• 核参数平滑后，可以提升一点点鲁棒性，说明高频信息是对抗攻击的一部分，但并非全部，可能还有其他因素
• CNN高频成分引入的多少，可能会导致精度和鲁棒性之间的平衡

总结

本文从数据的高低频成分角度分析，得出如下结论：

• CNN学习过程中会先尝试拟合低频信息，随着训练进行如果loss不再下降，则会进一步引入高频成分
• 高频成分不仅仅是噪声，还可能包含和数据分布特性相关信息，但是CNN无法针对性的选择利用，如果噪声引入的程度比较多则会出现过拟合，泛化能力下降
• 暂时没有一个好手段去除高频成分中的噪声，目前唯一能做的就是尝试用合适的半径阈值r去掉高频成分，防止噪声干扰，同时测试也需要进行相应去高频操作，或许可以提升泛化能力
• mix-up、BN、对抗样本和早停止等提点组件都可以促进CNN尽可能快且多的利用高频成分，从而提升性能
• 对抗鲁棒性较好的模型卷积核更加平滑，可以利用该特性稍微提高下CNN的鲁棒性

最后重申一句：人类标注时候仅仅是考虑低频语义信息，而CNN学习会考虑额外的高频成分，从而学习出的模型表现有时候不符合人类想法，这不是bug，也不是CNN垃圾，而是大家看到的和想的不一样。

噪声label学习

论文名称：Identifying Mislabeled Data using the Area Under the Margin Ranking

github：https://github.com/Manuscrit/Area-Under-the-Margin-Ranking

论文思想

论文目的主要是找出错误标注数据。主要创新包括：

(1) 提出了aum分值 Area Under the Margin来区分正确和错误标注样本 (2) 由于aum分值是和数据集相关的，阈值切分比较关键，故作者提出指示样本indicator samples的概念来自动找到最合适的aum阈值

Not all data in a typical training set help with generalization

AUM的定义非常简单：

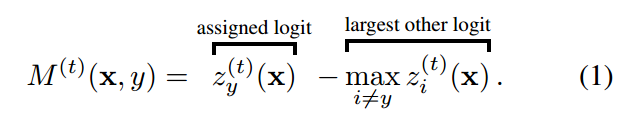
对于任何一个样本，z是指softmax预测概率值，zy是指的分配label位置对应的预测输出值，max zi是指除了label位置预测输出最大值。当样本label正确时候，该值比较大，当label不正确的时候，该值比较小甚至是负数。

利用该特性就可以把错误标签样本找出来。仅仅计算样本当前epoch时候的AUM值不太靠谱，一个错误样本应该aum值都差不多，故作者采用了所有epoch的aum平均值：

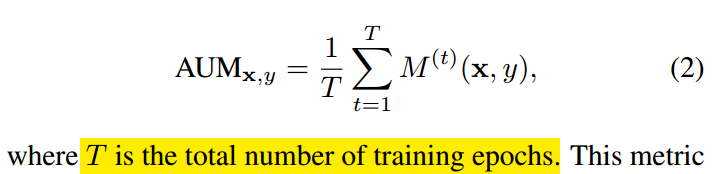
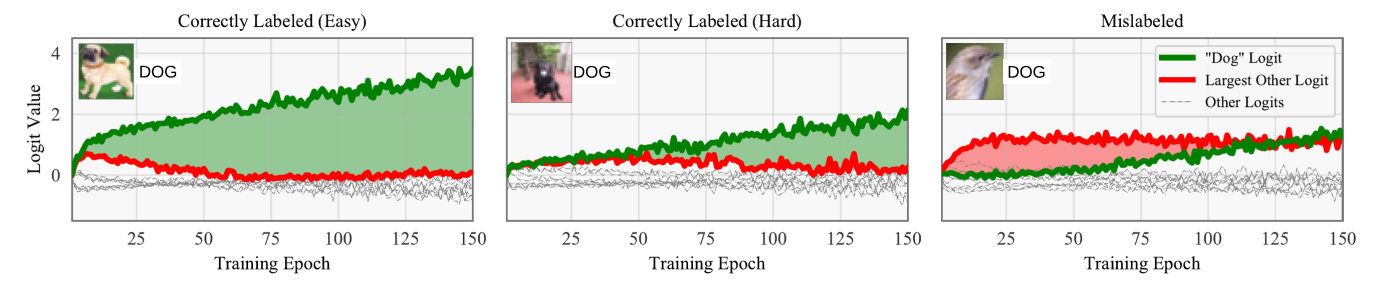
中间的绿色区域就是AUM。

基于上述办法可以得到每个样本的AUM值，但是如何设置阈值来确定噪声样本？本文提出Indicator Samples概念自动确定阈值。

做法其实非常简单：挑选一部分正确label数据，然后把这些数据全部算作c+1类，相当于在原始类别基础上扩展一个类，可以发现这些样本数据其实全部算是错误label数据，可以利用这部分数据的aum值来作为阈值。

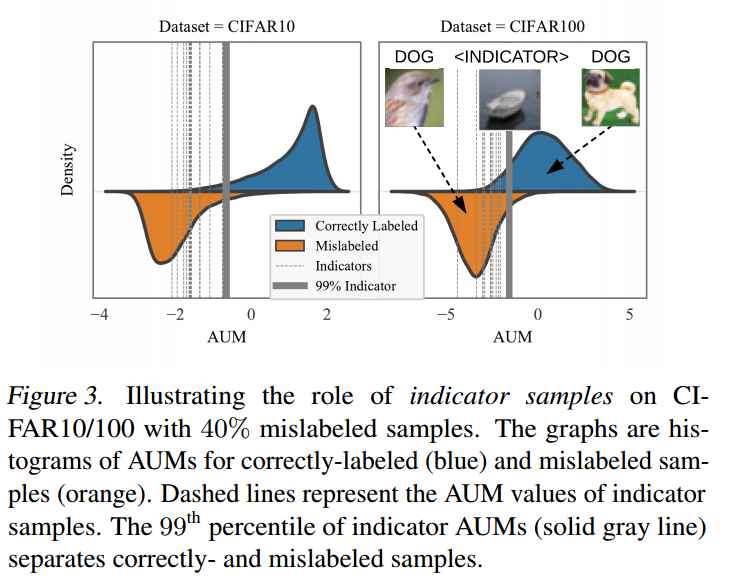
得到这些样本的aum值后，选择第99百分位数作为阈值即可，小于阈值的就是噪声样本。

算法流程

需要注意的是上述过程需要不断迭代，并且每次迭代所选择的指示样本都不一样，这样才能有效挖掘出来所以噪声样本。 并且不能在过拟合很严重时候计算aum，作者采用的是在第一次学习率下降时候统计aum。

实验采用的是ResNet-32，300 epochs using 10−4 weight decay, SGD with Nesterov momentum, a learning rate of 0.1, and a batch size of 256。The learning rate is dropped by a factor of 10 at epochs 150 and 225.

When computing the AUM to identify mislabeled data, we train these models up until the first learning rate drop (150 epochs)，并且把batch size变成64，主要是增加sgd训练时候的方差，对统计aum有好处。在移除错误样本后，再采用上述策略进行训练。

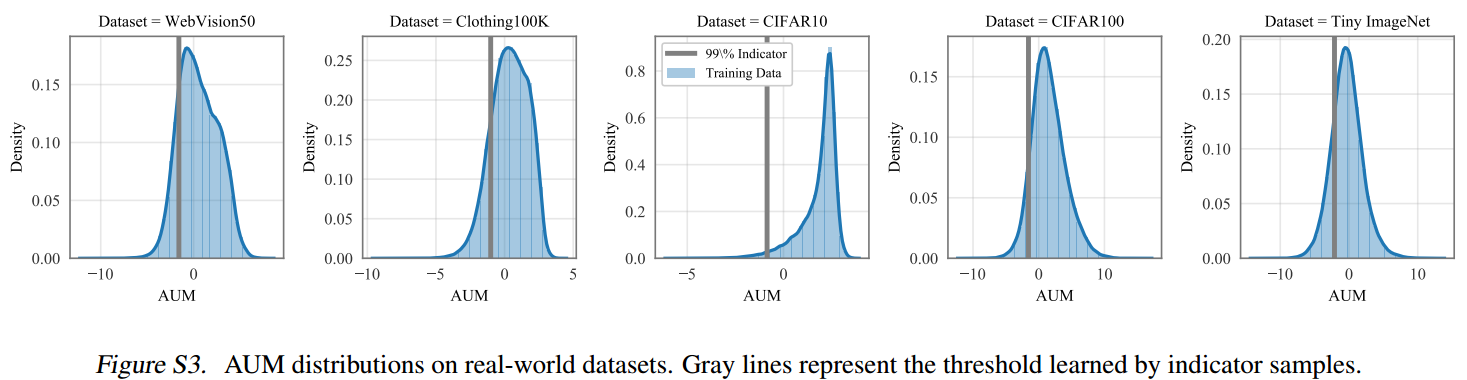
网络泛化能力

论文名称：understanding deep learning requires rethinking generalization

github：https://github.com/pluskid/fitting-random-labels

论文思想

这篇论文就是想要讨论为什么有的网络泛化能力比较好，而有的却不是很好。做了以下实验：

1. Randomization tests
2. The role of explicit regularization
3. Finite sample expressivity
4. The role of implicit regularization

Randomization tests

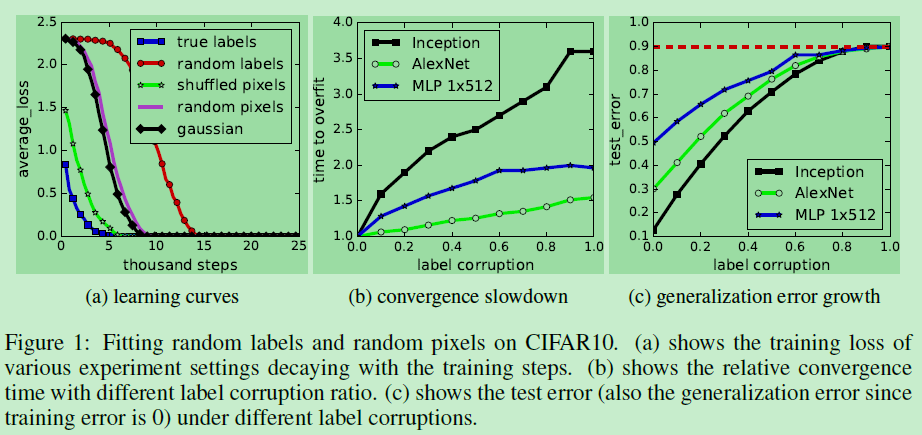
这个部分的实验对训练数据进行污染，然后观察网络在污染的训练数据上的训练结果。按照不同的污染手段和污染程度，具体有这些实验：

• True label：无污染，原始数据

• 标签污染：

• • Partially corrupted labels：对每个样本的真实标签以一定概率替换为一个随机类别标签
  • Random labels：所有样本的真实标签都替换为随机的类别标签

• 样本污染：

• • Shuffled pixels：随机选择一种像素顺序，以这个顺序重排所有训练和测试样本的像素
  • Random pixels： 对每个样本各随机应用一种像素顺序
  • Gaussian：对每一个样本，用和原样本一样均值和方差的高斯分布随机生成随机的图片

论文中说，对于不同污染的数据，用的是同样的训练超参进行的训练，实验结果简单来说就是，不管怎么对数据动手脚，网络都能把训练误差学到0（图a）。不过，随着数据污染的加重，网络的收敛速度变慢（图b），泛化能力也变差（图c）。

接着论文表示，之前对于泛化能力的理论并不能很好地解释现实情况。一方面是指的VC dimension、Rademacher complexity和uniform stability这些之前的工作。另一方面就是下一部分对于正则的实验结果。

（这里由于原文里没有具体说VC dimension、Rademacher complexity和uniform stability这些之前的工作不能解释实验结果的原因，我说一下我的理解，按照之前的理论，深层的神经网络复杂度是很高的，很容易过拟合，这和实验中拟合随机标签是符合的。但是没法解释一般情况下深层网络的泛化能力从何而来。）

The role of explicit regularization

一般我们认为在模型参数比较多的时候，加入正则是一种比较好的防止过拟合的方法。因为当模型比较复杂的时候，假设空间会变得巨大，而正则帮助我们对假设空间进行了“剪枝”。这篇论文使用了几种神经网络中比较常用的正则方法：

• 显式的正则：

• • Data augmentation，Weight decay和Dropout。

• 隐式的正则：

• • Early stop，Batch normalization

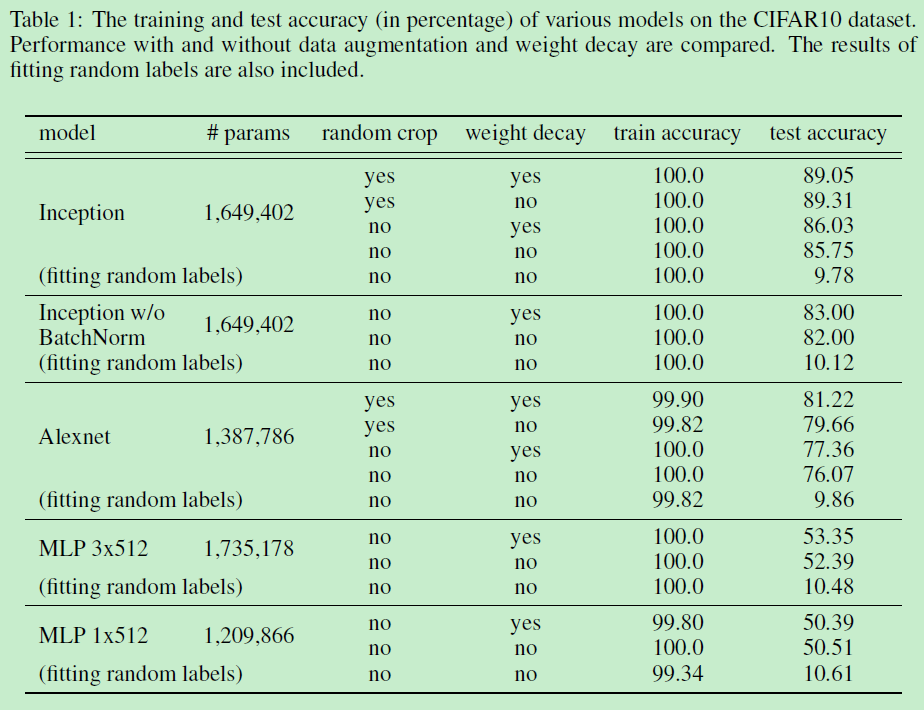
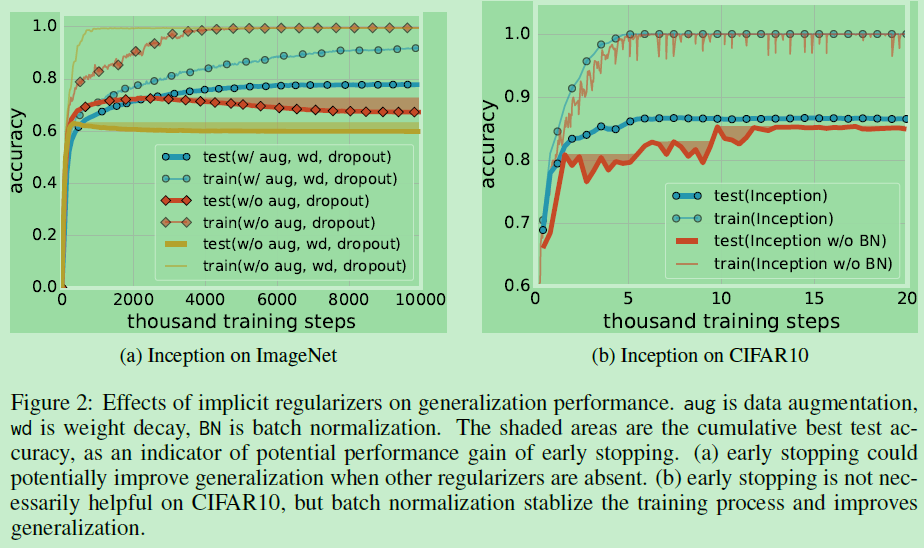
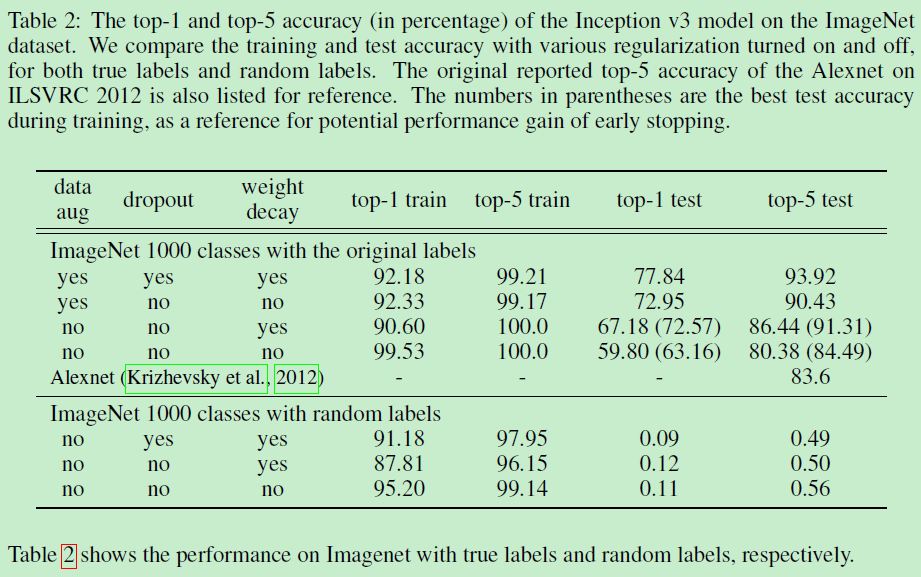
实验的结果比较多，但是结论比较简单，这篇论文觉得虽然这些正则方法确实能提高网络的泛化能力，但是正则方法并不是网络有较好泛化能力的关键，因为网络去掉这些正则方法，也能取得一个还不错的结果；同时，网络依靠正则化提高的泛化能力，可能还不如换另一种网络结构提高得多。

Finite sample expressivity

这篇论文认为之前大部分对于神经网络的表达能力的工作都太侧重于“population level”的结论。这篇论文认为与实践中更相关的应该是在有限样本情况下神经网络的表达能力。并得出了一个结论：

The role of implicit regularization

最后这篇论文以一个线性模型为例，讨论了SGD（stochastic gradient descent）本身带有隐含的正则化作用。

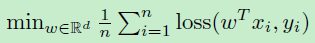
这篇论文从一个普通的经验风险最小开始，$n$为样本数量，假设$x_i$是一个$d$维的特征向量。（论文中说）当$d\ge n$时我们可以拟合任何标签，那么这样一个模型是否能在没有正则方法的情况下有泛化能力呢？

如果令$X$是一个$n\times d$的样本矩阵，秩为$n$，无论什么样的$y$，等式有$Xw=y$无数种解。我们可以解这个线性系统得到上面经验风险最小问题的一个全局最小。但是是否所有的解都有一样的泛化能力？是否有一个方法能决定某个全局最小解比另一个泛化能力好？这篇论文中接着讨论了SGD是如何选择的。SGD对参数的更新可以表示为：$w_{t+1}=w_t-\eta_t e_tx_{i_t}$，其中$\eta$是步长，$e$是预测误差。所以如果偏置项为0的话，最后的解肯定可以以这个形式表示：$w=\sum_{i=1}^{n}\alpha_ix_i=X^T\alpha$。如果我们再完全拟合了标签$Xw=y$，那么可以得到这$XX^T\alpha =y$,个等式有唯一解。可以注意到，这个等式只依赖于样本之间的点积。

当数据少于10w时，这个线性系统可以在一个工作站上求解。这篇论文在MNIST数据集上求解$XX^T\alpha =y$得到了1.2%的测试误差。在CIFAR10上，使用了高斯核得到了46%的测试误差。论文里做了一些处理以后，这两个性能还能提升。而且论文里还说加正则并不能提高多少性能。总而言之，论文求解方程得到一个完全拟合训练集的线性模型，而这个线性模型泛化能力还不错。

总结

Deep neural networks easily fit random labels，同时正则化可以避免过拟合，但是并非必须。

论文要讨论的是神经网络的泛化能力从何而来。

先用神经网络暴力拟合开始，实验神经网络有能力对数据进行暴力拟合（虽然这一点本身就有争议。。），这一点是想说明神经网络复杂度确实很高，也有能力学成一个泛化能力很差的模型。

接着论文考察了一下一般正则化方法对泛化能力的提升，发现提升有限；没有正则化方法，网络也能有一个还行的泛化能力。结合前一个实验，这说明网络虽然可以暴力拟合，但是一般情况下，它并没有这么干。

所以问题就来了：为什么会变成这样呢，明明是有限的训练集，明明有能力暴力拟合数据的，本该就这样直接记住训练集的，为什么你还学到了泛化能力。

最后以线性模型为例（这一点也有很多不服的），认为SGD的过程本身带有一个隐含的正则效果。就是说优化方法本身限制了模型的解空间，使得学到的模型有一个基础的泛化能力。